競賽的意義

最近在想，為何競賽沒被幾個AI優勢的大公司分據，在這篇得到啟發

有點類似一滴血所談的靈敏度與特異性
https://known.ifeng.com/a/20190625/45510060_0.shtml

闻里提到这个检查的准确率是95%，但这并不是专业词汇。有两个比较关键的跟检测、诊断有关的概念：灵敏度和特异性。

灵敏度：癌症患者被正确检查出来的比例。

特异性：健康人中检查结果正常的比例。

新闻里使用的这个“准确率”比较含混，不知道指的是灵敏度还是特异性。不妨假设这个检查能达到95%的灵敏度，95%的特异性。

如果是考试，这已经是学霸的成绩了，但是用在癌症筛查上，会是什么效果呢？

为了简单说明这个问题，我们假设癌症的发病率是每10万中有100人。

用这个检查，这100个癌症患者中，有95个都能被查出来。看来很不错。

但是，在99900个健康人中，因为检查的特异性只有95%，意味着有5%的人也会被误诊为癌症，所以误诊总人数会有4995人。

所以说，每正确查出一个患者，就会误诊52人。

https://www.infoq.cn/article/rlxe9VmwWK3zjjGL2Vgg

Epi101 来救场啦。多重假设检验在医学上确实很常见，尤其是在基因组学等“大数据”领域。我们已经用了几十年学习如何处理这些问题。解决这类问题最简单可靠的方法被称为 Bonferroni 校正 ^^。

Bonferroni 校正特别简单：将 p 值除以测试次数就得到“统计显著性阈值”，该阈值已经针对所有额外的硬币投掷进行了调整。因此，在这种情况下，我们计算 0.5/500 的值。新的 p 值目标是 0.0001，任何比这个差的值将被认为是支持零假设（即竞争对手在测试集上的表现同样出色）。我们把这个值放入我们的指数计数器。

要有一个没有偏差的测试集，只有一种方法，就是包括全部人！然后，无论什么模型，在测试中表现良好的也将是实践中最好的，因为我们在所有可能的未来病患身上做了测试（看起来很难）。

这导致了一个非常简单的想法，即随着测试集变得更大，我们的测试结果会变得更可靠。实际上，我们可以通过指数计算来预测测试集的可靠性。

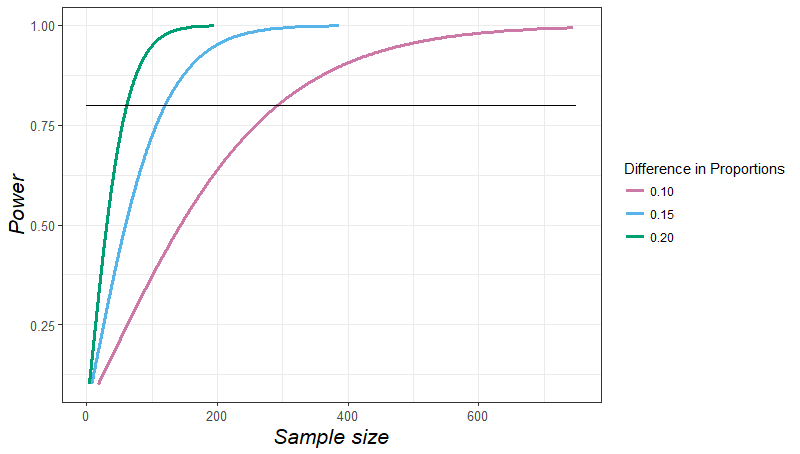
这是指数曲线。如果我们有个关于我们的“获胜”模型比次优模型好多少的大概想法，那么，我们可以估计我们需要多少测试病例，以便可靠地表明它更好。

因此，要表明我们的模型比竞争对手的好 10%，我们就需要大约 300 个测试病例。我们还可以看到，随着模型之间的差异变得越来越小，所需的病例数量如何呈指数级增长。