精選文章
- 取得連結
- X
- 以電子郵件傳送
- 其他應用程式
中本聰: Bitcoin: A Peer-to-Peer Electronic Cash System
心得:
- 建立雙方信任的方式 -> 零知識證明
- 建構在 Hash 上是否有風險?
- 聰明人很多, 比特幣的確有人用彩虹表來做
- 所以後來的使用 hmac 方式, 加入 salt 參數來做 hash, 以避免彩虹表
- 中國前幾年增大算力, 想藉此變成大多數的算力結點, 攻破最長鍊
歐美發現也加緊增大算力, 帶動一波比特幣高潮
今年中國放棄算力攻佔計畫?, 打算推動自己的數位人民幣
如果是這樣, 一旦中國變成算力 > 其他誠實節點時,
挖礦的獎勵不足以支撐他要破壞比特幣的動機.
- 現在比特幣很貴, 要實驗成本高. 可能找其他虛擬貨幣如狗狗幣來進一步應證.
--
Bitcoin: A Peer-to-Peer Electronic Cash System
比特幣: 點對點電子現金系統
Satoshi Nakamoto
中本聰
--
https://bitcoin.org/bitcoin.pdf
一個完全的點對點現金交易系統, 需要能直接兩方交易, 不用透過金融機構.
數位簽章技術實現了這一部分, 但若仍需公證的第三方來避免雙重支付的話,
就失去了這方案的優勢. 對於此雙重支付問題, 提出一個解決的方案,
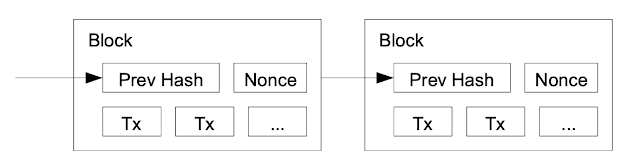
透過對每筆交易做時間戳記(timestamp), 將每筆交易經過雜湊(hash)運算後, 加到由「基於雜湊的工作量證明」(hash-based-proof-work)組成的鏈(chain)上。
除非重做所有的工作量證明,否則這些紀錄將不能被更改。
這長鍊不僅見證事件, 也證明這是來自很大的算力.
只要大多數節點上的算力, 不是用來攻擊這個網路的話,
這會產生一條最長鍊, 超過其他攻擊者.
這網路本身需要的基礎建設很少, 訊息會依據最大努力原則廣播出去,
結點可以自由選擇離開或重新加入.
並承認最長的工作量證明鏈, 作為節點離開時所發生的交易事件之證明。--
第一章: 簡介
電子商務仰賴傳統金融機構來做電子交易. 雖然傳統金融系統對大多電子交易是足夠的,
但仍有信任基礎上的弱點. 目前仍有需要金融機構介入調停處理的情況, 完全不可逆的電子交易
現實上並不存在. 這些調解成本提高了交易成本, 限制了最小交易單位, 無法用於小額支付;
也因為這系統無法提供不可逆的交易服務, 需要支付更大的成本.
因為交易有被撤銷的可能, 對信任的需求將會變得更廣泛.
商家對客戶會更加謹慎, 例如索取不必要的個人資訊,
並將一定比例的詐騙視為無法避免列入成本.
使用實體貨幣可以避免這些成本和支付的不確定性,
但不透過可信任的第三者的溝通管道並不存在.
我們需要的是用加密證明取代信任的電子交易系統, 允許有意願的雙方直接交易,
不需要第三者. 交易運算不可逆的方式可以避免賣家受騙, 而常規性託管機制,
可以輕易地保護買家. 在這篇論文, 我們對雙重支付問題, 提出一個解決方案.
透過點對點的分散式時間戳記伺服器去產生按時間排序的交易之計算證明,
只要誠實的節點比攻擊者控制更多的算力的話, 這系統會是安全的.
--
第二章: 交易
我們將電子貨幣定義為一串數位簽章, 每位付款者將前一次的交易 + 收款者的公鑰
做成電子簽章(用付款者私鑰加密), 放在貨幣的尾端交給收款者,
而收款者可用付款者的公鑰來做電子簽章的身份認證.
但這方式的問題在於收款者無法確定付款者先前是否已經支付用掉, 而有雙重支付的問題.
一般方式是導入可信任的中央權威機構, 或造幣廠, 來確認是否有雙重支付. 交易之後,
硬幣需要交還造幣廠來發行新幣, 且只有直接從造幣廠發行的新幣才能被信任,
沒有雙重支付的問題. 這方式的問題在於必須仰賴造幣廠, 就像仰賴銀行.
我們需要一個方式提供給收款者, 來證明先前付款者並未用此支付過.
因為我們針對的是之前的交易, 所以不用在意之後是否有雙重支付.
確認沒有漏列交易的方法, 就是去知道所有的交易. 而以造幣廠為基礎的模式中,
造幣廠必須知道所有的交易, 並決定交易先後順序.
若要在沒有信任的第三者下達到這目地的話, 交易本身必須公開.
我們需要有個系統, 讓所有參與者都接收同樣的交易順序.
收款者需要得到大多數節點的證明, 這交易是第一次發生的, 沒有雙重支付.
--
第三章: 時間戳記 timestamp server
從 timestamp server 開始談起. 將很多交易組成的區塊, 加上 timestamp 後做 hash,
並如同報紙或 Usenet 將其廣播. timestamp 證明了此資料在進入 hash 時的存在.
每個 timestamp 將前一個 timestamp 放進 hash, 形成一條鏈,
並用額外的 timestamp 來增強它.
 |
--
第四章: 工作量證明
為了在點對點下實現分散式時間戳記伺服器, 我們會需要一個類似 Adam Back's Hashcash 的工作量證明方式, 而非完全像 報紙或 Usenet 的發送方式. 這工作量證明, 包含像尋找一個值, 當用 SHA256 之後, 開頭會有一串 0. 一般來說, 隨著所需 0 的數目增加, 所需要的工作量會是指數增長. 而這證明時工作量會很小, 只需執行一次 hash 即可完成驗證.
在我們的時間戳記網路下, 工作量證明是指藉由增加區塊中的 nonce 數量, 直到這區塊的 hash 有足夠數量的 0. 一旦這計算完成工作量證明, 除非重新完成一定的工作量否則該區塊無法被更改.
若之後的區塊被鏈上, 修改區塊的工作量, 會包含所有之後鏈上的區塊
這工作量證明也解決了多數決代表的問題. 如果多數是建立在一個 IP 位址一票下,
則會被擁有需多 IP的所推翻. 所以工作量證明基本上是一個 CPU 一票. 多數決代表著最長的鏈.
而這最長鍊有著最多的需要工作量. 如果大多數的算力是由誠實的節點所控制的話,
這條誠實練增長的速度最快, 會超過其他競爭鍊. 若要修改一個先前的區塊,
攻擊者必須完成該區塊和鏈接之後的所有區塊的工作量證明, 並趕上和超越誠實節點的工作量證明. 稍後會說明, 較慢的攻擊者趕上的機率, 會隨著之後區塊的增加, 機率呈現指數性的下降.
考慮因硬體速度的增加及節點參與網路的程度起伏,工作量證明的難度是由每小時平均產生之區塊數量決定。如果區塊產生越快速,難度隨之增加.
--
第五章 網路
網路運作步驟:
1. 新的交易會被廣播給所有節點
2. 每個節點會收集加入新交易到區塊中
3. 每個節點對區塊找到一個困難的工作量證明
4. 當節點找到該工作量證明的區塊, 廣播此區塊給所有節點
5. 只有此區塊的交易都是有效, 尚未使用, 節點才會接受此區塊
6. 節點會使用先前已接納區塊的Hash, 作為之前Hash, 來往後鏈結接受此新區塊
節點總將最長的鏈當作是正確的, 來持續延展. 如果兩個節點同時廣播兩個不同版本的新區塊,
部分節點會先接受到其中之一, 這時先來的優先, 但也會保存另一條鏈. 當下一個工作量證明被找到時, 會切換到較長的鏈繼續處理.
新的交易廣播不需要觸及所有節點, 只要廣播到足夠的節點就會被整合到一個區塊中.
區塊廣播同樣允許漏掉訊息. 如果有節點沒有收到該區塊, 當它收到下一個區塊時,
會意識到遺漏了該區塊, 並發出請求該區塊的訊息.
--
第六章 獎勵
依照慣例, 區塊的第一個交易比較特別, 是代表這個新貨幣, 屬於這個區塊的發現建立者所有.
這激勵了節點去支持這個網路系統. 在沒有中央權威機構發行貨幣下, 提供了一個初期貨幣流通的方式. (節點自身可當造幣廠) 新貨幣數量的穩定增長, 和礦工挖黃金來增加流通類似. 在這案例,
花費的資源是 運算成本 和 電力.
交易手續費也是獎勵的一種. 如果交易的輸出值 < 輸入值, 差值為手續費記錄在這區塊
提供給交易所. 當有一定的數量流通時, 獎勵機制就可以完全依靠交易手續費, 避免通貨膨脹.
獎勵機制也可鼓勵節點要誠實, 如果有個貪婪的攻擊者, 有著比其他誠實節點都多的算力時,
可以選擇欺騙達到雙重支付, 或來挖礦. 他會發現挖礦賺得比較多, 而不會來破壞系統和自身貨幣的合法性.
--
第七章 回收磁碟空間
當一個貨幣的最後交易被整合進足夠的區塊中時, 則可丟棄在此資料前的交易,
以節省磁碟空間. 為不破壞區塊的 hash, 這些交易會被 hash 到 Merkle Tree.
只有 Merkle Tree 的 root hash 會被記錄到 區塊的 hash 中.
舊區塊可以透過去除樹的分支來壓縮大小, 而樹內部的 hash 不需要被保留.
不含交易內容的區塊標頭為 80 bytes. 假設每十分鐘產生一個區塊, 每年會需要
80 bytes * 6 * 24 * 365 = 4.2Mb
所以區塊標頭保存在記憶體不是問題.
--
第八章 簡化的支付驗證
驗證支付不需要所有節點運行, 使用者只需要保存最長的工作量證明練的標頭副本即可.
使用者可以不斷詢問網路節點, 直到相信所持有的是最長鍊. 而後透過 Merkle Tree 分枝
鏈結到此區塊並打上 timestamp. 使用者雖無法自行檢查交易, 但鏈結進之後, 可以看到
網路節點已經接受此交易, (因為改變工作量證明要包含之後區塊)
且之後的區塊也能證明此網路系統已接受過這筆交易.
因此, 只要誠實節點控制網路系統, 驗證會是可靠的, 反之會比較薄弱.
因為網路節點可以自行驗證交易, 攻擊者若掌握此網路系統, 此簡易驗證方法,
會被攻擊者拿來做交易欺騙. 解決方法之一是, 當發現無效的區塊時, 發出警報通知.
驅使使用者下載所有區塊資料來比對. 對於有頻繁支付特性的商業機構而言,
會想要有自己的節點, 以有獨立的安全性和快速交易的便利性.
第九章 幣值的結合與分割
雖可個別處理貨幣, 但對同筆轉帳下的每分錢都分別建立單獨的交易是很麻煩的.
為了讓幣值可以分割和結合, 交易會有多筆輸入輸出. 通常來自前次大筆的單一輸入,
或多筆小筆的輸入結合. 而輸出最多兩種, 付款和找零.
值得注意的是, 一個交易可能會有多筆交易, 而這交易本身可能又繼續延伸依賴其他交易.
但這不是問題. 因為我們並不需要取得一個完全獨立的交易歷史副本資料.
--
第十章 隱私
傳統銀行對此做法是, 限制參與者和第三方公正者取得這些資訊的權限.
雖然此篇方法需要公開所有交易, 但交易者公鑰是匿名的.
所以大家只知道有這些交易和交易內容, 但不曉得是誰.
這和股票交易類似. 可以知道交易時間和交易數量, 但不曉得交易雙方是誰.
有些仍難避免, 像同筆交易多重輸入, 這些輸入是同一個擁有者.
風險在於擁有者的公鑰被揭露時, 所有該擁有者的交易也會被找出來.
--
第十一章 計算
假設一種情況, 攻擊者比誠實鍊還快產生一條替代鍊.
即便這樣, 也無法讓此系統變成可任意變更, 讓攻擊者可以拿到新的貨幣, 或偽造交易.
節點不會接受無效的交易做為支付, 誠實節點也不會接受包含無效交易的區塊.
攻擊者只能試圖改變他剛剛的交易拿回貨幣.
誠實鏈和攻擊鍊可以視作二項隨機漫步 (binomial random walk), 可定義成
誠實鍊延展時 +1, 攻擊鍊延展時 -1.
攻擊鍊成功機率可以看作是賭徒破產問題 (Gambler's ruin problem)
假設 p > q , 則攻擊者成功機率, 會隨著區塊數量增加, 而指數下降.
所以須考慮的是, 交易者接受方需要等待多久, 才能確定發送者沒有竄改.
假設發送者是攻擊者, 想讓接收者相信已經支付給接受者一段時間了,
接著在一段時間後將這筆重新支付給自己. 接受者會收到警報,
但攻擊者會希望這警報為時已晚.
接受者產生一對新鑰, 並在簽章前提供新的公鑰給發送者, 這樣可以避免發送者預先
製作一條替代練, 持續運算直到幸運地比誠實鍊長時進行交易. 而需要等到交易送出,
才能開始運算替代鍊.
接受者會等到交易上區塊, 且後面接了 z 個區塊. 此時接收者不知道攻擊者實際的進展,
但假設每個誠實區塊以平均的預定時間產生, 則攻擊者可能的進展, 會是一個 Poisson 分佈(Poisson Distribution),分布的期望值為:
寫成 C 程式:
執行結果: 我們可以發現機率隨著後面所接的區塊個數 z, 而有指數下跌.
--
第十二章: 結論
我們提出一個不需要依賴信任的電子交易系統.
首先討論電子貨幣的數位簽章, 對所有權有很好的控制, 但無法解決雙重支付.
為解決此問題, 我們提出一個使用工作量證明的點對點網路系統, 來記錄公開歷史交易.
如果誠實節點擁有主要的算力, 攻擊者若要串改在運算上是不可行的.
這網路堅固之處在於它非結構化的簡易性. 節點工作時所需做得協調很少.
因為訊息不用被傳送到特定位置, 只要盡力傳送出去就好, 節點本身不用識別.
節點可以隨時自由離開或加入. 當節點不在網路上時, 接受用工作量證明鍊,
作為交易事件的紀錄證明. 用算力進行投票, 以延長練的方式來接受有效區塊,
拒絕處理無效區塊, 規則和獎勵可以依循這個共識機制.













留言
張貼留言